BisectDemo.m
Contents
Overview
Illustrates the bisection algorithm coded in bisect.m to solve 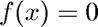 on
on ![$[a,b]$](BisectDemo_eq50527.png) . It is important that
. It is important that 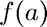 and
and 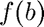 have opposite signs.
have opposite signs.
Find the first positive root of the Bessel function 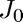
We use the built-in MATLAB function besselj to solve
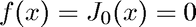
disp('Find the first positive root of the Bessel function J0:') J0 = @(x) besselj(0,x); disp('Initial interval is [a,b] = [0,3]') [x,iter] = bisect(J0,[0,3]); disp(sprintf('The first positive root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter))
Find the first positive root of the Bessel function J0: Initial interval is [a,b] = [0,3] x1 = 3.00000000000000 x2 = 3.00000000000000 x3 = 2.62500000000000 x4 = 2.43750000000000 x5 = 2.43750000000000 x6 = 2.43750000000000 x7 = 2.41406250000000 x8 = 2.41406250000000 x9 = 2.40820312500000 x10 = 2.40527343750000 x11 = 2.40527343750000 x12 = 2.40527343750000 x13 = 2.40490722656250 x14 = 2.40490722656250 x15 = 2.40490722656250 x16 = 2.40486145019531 x17 = 2.40483856201172 x18 = 2.40482711791992 x19 = 2.40482711791992 x20 = 2.40482711791992 x21 = 2.40482568740845 x22 = 2.40482568740845 x23 = 2.40482568740845 x24 = 2.40482568740845 x25 = 2.40482559800148 x26 = 2.40482559800148 x27 = 2.40482557564974 x28 = 2.40482556447387 x29 = 2.40482555888593 x30 = 2.40482555888593 x31 = 2.40482555888593 x32 = 2.40482555818744 x33 = 2.40482555783819 x34 = 2.40482555783819 x35 = 2.40482555775088 x36 = 2.40482555770723 x37 = 2.40482555770723 x38 = 2.40482555769631 x39 = 2.40482555769631 x40 = 2.40482555769631 x41 = 2.40482555769631 x42 = 2.40482555769631 x43 = 2.40482555769597 x44 = 2.40482555769580 x45 = 2.40482555769580 x46 = 2.40482555769580 x47 = 2.40482555769578 x48 = 2.40482555769578 x49 = 2.40482555769577 x50 = 2.40482555769577 x51 = 2.40482555769577 x52 = 2.40482555769577 The first positive root of J0 is x = 2.404826. It was computed in 52 iterations.
Compute 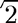
We solve the equation
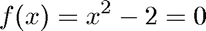
%pause disp('Compute sqrt(2):') sqr2 = @(x) x^2-2; disp('Initial interval is [a,b] = [0,2]') [x,iter] = bisect(sqr2,[0,2]); disp(sprintf('sqrt(2) = %f was computed in %d iterations.',x,iter))
Compute sqrt(2): Initial interval is [a,b] = [0,2] x1 = 2.00000000000000 x2 = 1.50000000000000 x3 = 1.50000000000000 x4 = 1.50000000000000 x5 = 1.43750000000000 x6 = 1.43750000000000 x7 = 1.42187500000000 x8 = 1.42187500000000 x9 = 1.41796875000000 x10 = 1.41601562500000 x11 = 1.41503906250000 x12 = 1.41455078125000 x13 = 1.41430664062500 x14 = 1.41430664062500 x15 = 1.41424560546875 x16 = 1.41421508789063 x17 = 1.41421508789063 x18 = 1.41421508789063 x19 = 1.41421508789063 x20 = 1.41421508789063 x21 = 1.41421413421631 x22 = 1.41421365737915 x23 = 1.41421365737915 x24 = 1.41421365737915 x25 = 1.41421359777451 x26 = 1.41421356797218 x27 = 1.41421356797218 x28 = 1.41421356797218 x29 = 1.41421356424689 x30 = 1.41421356238425 x31 = 1.41421356238425 x32 = 1.41421356238425 x33 = 1.41421356238425 x34 = 1.41421356238425 x35 = 1.41421356238425 x36 = 1.41421356238425 x37 = 1.41421356238425 x38 = 1.41421356237697 x39 = 1.41421356237333 x40 = 1.41421356237333 x41 = 1.41421356237333 x42 = 1.41421356237333 x43 = 1.41421356237311 x44 = 1.41421356237311 x45 = 1.41421356237311 x46 = 1.41421356237311 x47 = 1.41421356237311 x48 = 1.41421356237310 x49 = 1.41421356237310 x50 = 1.41421356237310 x51 = 1.41421356237310 x52 = 1.41421356237310 x53 = 1.41421356237310 sqrt(2) = 1.414214 was computed in 53 iterations.