IQIDemo.m

Contents

Overview

Illustrates the inverse quadratic interpolation method coded in iqi.m to solve 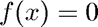$f(x)=0$ near the three initial guesses 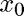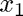$x_0$, $x_1$, and $x_2$.

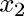Find a root of the Bessel function 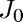$J_0$

We use the built-in MATLAB function besselj to solve

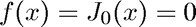
$$ f(x) = J_0(x) = 0 $$

Note that the inverse quadratic interpolation method requires two initial guesses. Here we use

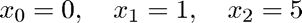
$$ x_0 = 0, \quad x_1 = 1, \quad x_2 = 5 $$

Note how iqi.m needs functions as input arguments.

disp('Find a root of the Bessel function J0:')
J0 = @(x) besselj(0,x);
disp('Initial guesses are x0 = 0, x1 = 1, x2 = 5')
[x,iter] = iqi(J0,[0 1 5]);
disp(sprintf('A root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter))

Find a root of the Bessel function J0:
Initial guesses are x0 = 0, x1 = 1, x2 = 5
x1 = 4.24837804522871
x2 = 5.22387379641461
x3 = 5.46191080362565
x4 = 5.51512765590600
x5 = 5.52006433089824
x6 = 5.52007810961385
x7 = 5.52007811028631
x8 = 5.52007811028631
x9 = 5.52007811028631
A root of J0 is x = 5.520078.
It was computed in 9 iterations.

Find the first positive root of the Bessel function 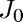$J_0$

Notice how the previous example did not produce the first positive root. In order to get that, we need to change our initial guess. We now use

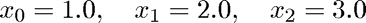
$$ x_0 = 1.0, \quad x_1 = 2.0, \quad x_2 = 3.0 $$

The rest is the same as above (and therefore not even repeated in the code).

%pause
disp('Find the first positive root of the Bessel function J0:')
disp('Initial guesses are x0 = 1, x1 = 2, x2 = 3')
[x,iter] = iqi(J0,[1 2 3]);
disp(sprintf('The first positive root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter))

Find the first positive root of the Bessel function J0:
Initial guesses are x0 = 1, x1 = 2, x2 = 3
x1 = 2.45020330258122
x2 = 2.40230484576990
x3 = 2.40480584854874
x4 = 2.40482555814647
x5 = 2.40482555769577
x6 = 2.40482555769577
The first positive root of J0 is x = 2.404826.
It was computed in 6 iterations.


© Greg Fasshauer, IIT. Published with MATLAB® 7.11