LSQquadSVD.m

Overview
Example 1: Solving the least squares problem using singular value decomposition
Example 1a: Fit using the pseudoinverse
Example 2: Fit "noisy" data using a quadratic polynomial
Example 2a: Fit "noisy" data using the pseudoinverse

Overview

Illustrates the use of the SVD for the computation of a polynomial least squares fit

Example 1: Solving the least squares problem using singular value decomposition

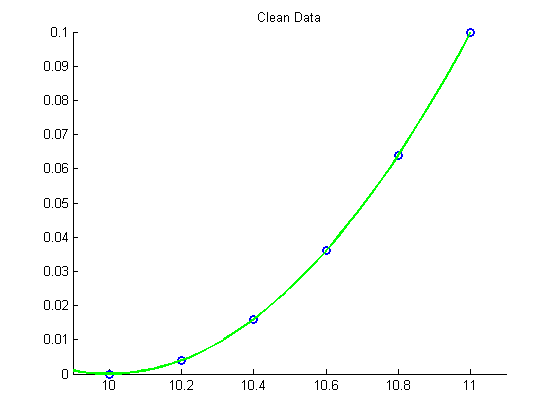
Data comes from the quadratic polynomial (no noise)

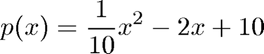
$p(x) = \frac{1}{10} x^2 -2x + 10$

clear all
close all
x = [10:0.2:11]';
disp('Clean Data')
y = [0:0.2:1]'.^2/10;
m = length(x);
hold on
plot(x, y, 'bo', 'LineWidth',2)
xlim([9.9 11.1])
ylim([0 0.1])
%pause
disp('Solving least squares problem with SVD')
A = [x.^2 x ones(m,1)]
% Compute the SVD of A
[U S V] = svd(A)
% find number of nonzero singular value = rank(A)
r = length(find(diag(S)))
Uhat = U(:,1:r)
Shat = S(1:r,1:r)
z = Shat\Uhat'*y;
% or
%z = Uhat'*y./diag(Shat);
c = V*z
xx = linspace(9.9,11.1,50);
yy = c(1)*xx.^2+c(2)*xx+c(3);
plot(xx, yy, 'g-', 'LineWidth', 2)
title('Clean Data')
disp('Fitting with quadratic polynomial')
disp(sprintf('p(x) = %3.2fx^2 + %3.2fx + %3.2f',c))
hold off

Clean Data
Solving least squares problem with SVD

A =

  100.0000   10.0000    1.0000
  104.0400   10.2000    1.0000
  108.1600   10.4000    1.0000
  112.3600   10.6000    1.0000
  116.6400   10.8000    1.0000
  121.0000   11.0000    1.0000


U =

    0.3693   -0.6076    0.5620   -0.1881   -0.0850   -0.3687
    0.3841   -0.3870   -0.0989    0.5732    0.3351    0.5020
    0.3993   -0.1575   -0.4326   -0.6543   -0.2266    0.3861
    0.4147    0.0809   -0.4392    0.4051   -0.4804   -0.4834
    0.4304    0.3283   -0.1185   -0.1994    0.7254   -0.3561
    0.4465    0.5847    0.5294    0.0635   -0.2685    0.3201


S =

  272.1416         0         0
         0    0.8447         0
         0         0    0.0022
         0         0         0
         0         0         0
         0         0         0


V =

    0.9955    0.0945    0.0089
    0.0945   -0.9778   -0.1872
    0.0090   -0.1872    0.9823


r =

     3


Uhat =

    0.3693   -0.6076    0.5620
    0.3841   -0.3870   -0.0989
    0.3993   -0.1575   -0.4326
    0.4147    0.0809   -0.4392
    0.4304    0.3283   -0.1185
    0.4465    0.5847    0.5294


Shat =

  272.1416         0         0
         0    0.8447         0
         0         0    0.0022


c =

    0.1000
   -2.0000
   10.0000

Fitting with quadratic polynomial
p(x) = 0.10x^2 + -2.00x + 10.00

Example 1a: Fit using the pseudoinverse

disp('Coefficients obtained directly with pseudoinverse')
pinvA = pinv(A);
c = pinvA*y

Coefficients obtained directly with pseudoinverse

c =

    0.1000
   -2.0000
   10.0000

Example 2: Fit "noisy" data using a quadratic polynomial

Note that again we do not need to re-compute the SVD of the matrix 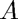$A$ for this part since the matrix 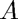$A$ is still the same. Only the data vector 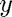$y$ has changed!

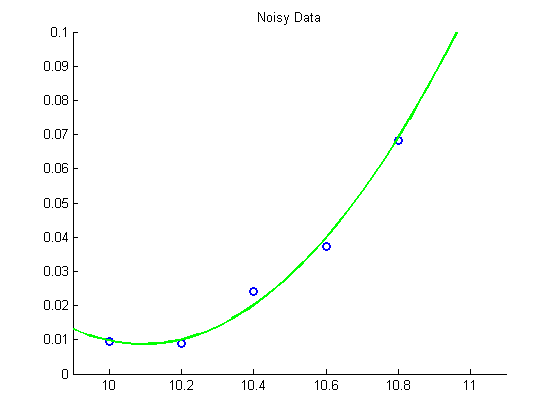
%pause
disp('Noisy Data')
% Add 10% noise to the data
y = y + 0.1*max(y)*rand(size(y));
figure
hold on
plot(x, y, 'bo', 'LineWidth',2)
xlim([9.9 11.1])
ylim([0 0.1])
%pause
disp('Solving noisy least squares problem with SVD')
% No need to re-compute the SVD of A since A is the same, only
% y has changed!
z = Shat\Uhat'*y;
c = V*z
xx = linspace(9.9,11.1,50);
yy = c(1)*xx.^2+c(2)*xx+c(3);
plot(xx, yy, 'g-', 'LineWidth', 2)
title('Noisy Data')
disp('Fitting with quadratic polynomial')
disp(sprintf('p(x) = %3.2fx^2 + %3.2fx + %3.2f',c))
hold off

Noisy Data
Solving noisy least squares problem with SVD

c =

    0.1209
   -2.4411
   12.3273

Fitting with quadratic polynomial
p(x) = 0.12x^2 + -2.44x + 12.33

Example 2a: Fit "noisy" data using the pseudoinverse

disp('Coefficients obtained directly with pseudoinverse (computed earlier)')
c = pinvA*y

Coefficients obtained directly with pseudoinverse (computed earlier)

c =

    0.1209
   -2.4411
   12.3273