Loss of Significance

Contents

This script demonstrates loss of significant digits and how to fix it for the specific example of evaluation of

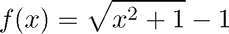
$$ f(x) = \sqrt{x^2+1}-1 $$

for increasingly smaller values of 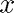$x$.

Number of trials

N = 15;

Result using double-precision

disp('Result using double precision')
for n=0:N
    x = 10^(-n);
    f = sqrt(x^2+1)-1;
    disp(sprintf('x=%f,  sqrt(x^2+1)-1 = %e',x,f))
end

Result using double precision
x=1.000000,  sqrt(x^2+1)-1 = 4.142136e-001
x=0.100000,  sqrt(x^2+1)-1 = 4.987562e-003
x=0.010000,  sqrt(x^2+1)-1 = 4.999875e-005
x=0.001000,  sqrt(x^2+1)-1 = 4.999999e-007
x=0.000100,  sqrt(x^2+1)-1 = 5.000000e-009
x=0.000010,  sqrt(x^2+1)-1 = 5.000000e-011
x=0.000001,  sqrt(x^2+1)-1 = 5.000445e-013
x=0.000000,  sqrt(x^2+1)-1 = 4.884981e-015
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000

Using single-precision

Here is where we see the problems

pause
disp('Result using single precision')
for n=0:N
    x = 10^(-n);
    f = single(sqrt(x^2+1))-1;
    disp(sprintf('x=%f,  sqrt(x^2+1)-1 = %e',x,f))
end

Result using single precision
x=1.000000,  sqrt(x^2+1)-1 = 4.142135e-001
x=0.100000,  sqrt(x^2+1)-1 = 4.987597e-003
x=0.010000,  sqrt(x^2+1)-1 = 4.994869e-005
x=0.001000,  sqrt(x^2+1)-1 = 4.768372e-007
x=0.000100,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000010,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000001,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000
x=0.000000,  sqrt(x^2+1)-1 = 0.000000e+000

Using single-precision, but fixed

pause
disp('Result using single precision, but fixed')
for n=0:N
    x = 10^(-n);
    f = single(x^2)/(single(sqrt(x^2+1))+1);
    disp(sprintf('x=%f,  x^2/(sqrt(x^2+1)+1) = %e',x,f))
end

Result using single precision, but fixed
x=1.000000,  x^2/(sqrt(x^2+1)+1) = 4.142135e-001
x=0.100000,  x^2/(sqrt(x^2+1)+1) = 4.987562e-003
x=0.010000,  x^2/(sqrt(x^2+1)+1) = 4.999875e-005
x=0.001000,  x^2/(sqrt(x^2+1)+1) = 4.999999e-007
x=0.000100,  x^2/(sqrt(x^2+1)+1) = 5.000000e-009
x=0.000010,  x^2/(sqrt(x^2+1)+1) = 5.000000e-011
x=0.000001,  x^2/(sqrt(x^2+1)+1) = 5.000000e-013
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-015
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-017
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-019
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-021
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-023
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-025
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-027
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-029
x=0.000000,  x^2/(sqrt(x^2+1)+1) = 5.000000e-031


© Greg Fasshauer, IIT. Published with MATLAB® 7.11