NewtonDemo.m

Contents

Overview

Illustrates Newton's method coded in newton.m to solve 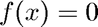$f(x)=0$ near the initial guess $x_0$.

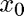Find a root of the Bessel function 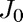$J_0$

We use the built-in MATLAB function besselj to solve

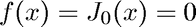
$$ f(x) = J_0(x) = 0 $$

Note that Newton's method also requires the derivative

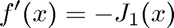
$$ f'(x) = -J_1(x) $$

and an initial guess. Here we use

$$ x_0 = 0.1 $$

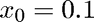
Note how newton.m needs functions as input arguments.

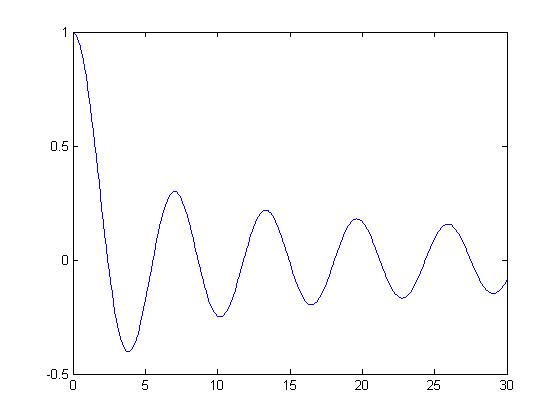
disp('Find a root of the Bessel function J0:')
J0 = @(x) besselj(0,x);
J0prime = @(x) -besselj(1,x);
disp('Initial guess is x0 = 0.1')
[x,iter] = newton(J0,J0prime,0.1);
disp(sprintf('A root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter))
x = [0:.1:30];
plot(x, besselj(0,x))

Find a root of the Bessel function J0:
Initial guess is x0 = 0.1
x1 = 20.07498957681857
x2 = 22.12298141969568
x3 = 20.79398411189246
x4 = 21.23307459842233
x5 = 21.21162251204526
x6 = 21.21163662987456
x7 = 21.21163662987926
x8 = 21.21163662987926
A root of J0 is x = 21.211637.
It was computed in 8 iterations.

Find the first positive root of the Bessel function 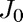$J_0$

Notice how the previous example did not produce the first positive root. In order to get that, we need to change our initial guess. We now use

$$ x_0 = 1.0 $$

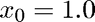
The rest is the same as above (and therefore not even repeated in the code).

%pause
disp('Find the first positive root of the Bessel function J0:')
disp('Initial guess is x0 = 1.0')
[x,iter] = newton(J0,J0prime,1);
disp(sprintf('The first positive root of J0 is x = %f.\nIt was computed in %d iterations.\n',x,iter))
%pause

Find the first positive root of the Bessel function J0:
Initial guess is x0 = 1.0
x1 = 2.73888573574470
x2 = 2.36778795983232
x3 = 2.40455555120498
x4 = 2.40482554254401
x5 = 2.40482555769577
x6 = 2.40482555769577
The first positive root of J0 is x = 2.404826.
It was computed in 6 iterations.

Compute 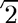$\sqrt{2}$

We solve the equation

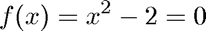
$$ f(x) = x^2 - 2 = 0 $$

where we again need the derivative

$$ f'(x) = 2x $$

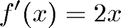
We use three different initial guesses:

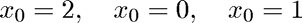
$$ x_0 = 2, \quad x_0 = 0, \quad x_0 = 1 $$

disp('Compute sqrt(2):')
sqr2 = @(x) x^2-2;
sqr2prime = @(x) 2*x;
disp('Initial guess is x0 = 2.0')
[x,iter] = newton(sqr2,sqr2prime,2);
disp(sprintf('sqrt(2) = %f was computed in %d iterations.\n',x,iter))

%pause
disp('Initial guess is x0 = 0')
[x,iter] = newton(sqr2,sqr2prime,0);

%pause
disp('Initial guess is x0 = 1.0')
[x,iter] = newton(sqr2,sqr2prime,1);
disp(sprintf('sqrt(2) = %f was computed in %d iterations.\n',x,iter))

Compute sqrt(2):
Initial guess is x0 = 2.0
x1 = 1.50000000000000
x2 = 1.41666666666667
x3 = 1.41421568627451
x4 = 1.41421356237469
x5 = 1.41421356237310
x6 = 1.41421356237309
sqrt(2) = 1.414214 was computed in 6 iterations.

Initial guess is x0 = 0
Newton iteration failed since derivative is zero.

Initial guess is x0 = 1.0
x1 = 1.50000000000000
x2 = 1.41666666666667
x3 = 1.41421568627451
x4 = 1.41421356237469
x5 = 1.41421356237310
x6 = 1.41421356237309
sqrt(2) = 1.414214 was computed in 6 iterations.


© Greg Fasshauer, IIT. Published with MATLAB® 7.11