NewtonmvDemo.m

Contents

Overview

Illustrates the multivariate Newton method with two examples. The multivariate Newton method is coded in newtonmv.m

First Example: Missile intercept problem

Function and Jacobian are provided in missile_f.m and missile_j.m.

disp('Solving missile intercept problem')
x0 = [1 1]';
disp(sprintf('Initial guess: x0 = [%f %f]',x0))
tol = 1e-8;
[root,iter] = newtonmv(x0, @missile_f, @missile_j, tol);
disp(' ')
%pause

Solving missile intercept problem
Initial guess: x0 = [1.000000 1.000000]
Iteration 1: approx root = [0.638625,0.980601]
Iteration 2: approx root = [0.627269,0.936045]
Iteration 3: approx root = [0.627860,0.936376]
Iteration 4: approx root = [0.627860,0.936376]
 

Second example: Intersection of circle and hyperbola

Uses circhyp_f.m and circhyp_j.m

% Find four solutions of circle hyperbola intersection

Trial 1

disp('Trial 1 of circle-hyperbola intersection problem')
x0 = [3 -1.5]';
disp(sprintf('Initial guess: x0 = [%f %f]',x0))
tol = 1e-8;
[root,iter] = newtonmv(x0, @circhyp_f, @circhyp_j, tol);
disp(' ')

Trial 1 of circle-hyperbola intersection problem
Initial guess: x0 = [3.000000 -1.500000]
Iteration 1: approx root = [2.611111,0.138889]
Iteration 2: approx root = [2.053257,0.412652]
Iteration 3: approx root = [1.939689,0.509855]
Iteration 4: approx root = [1.931894,0.517595]
Iteration 5: approx root = [1.931852,0.517638]
 

Trial 2

%pause
disp('Trial 2 of circle-hyperbola intersection problem')
x0 = [0 3]';
disp(sprintf('Initial guess: x0 = [%f %f]',x0))
[root,iter] = newtonmv(x0, @circhyp_f, @circhyp_j, tol);
disp(' ')

Trial 2 of circle-hyperbola intersection problem
Initial guess: x0 = [0.000000 3.000000]
Iteration 1: approx root = [0.333333,2.166667]
Iteration 2: approx root = [0.493939,1.956061]
Iteration 3: approx root = [0.517246,1.932244]
Iteration 4: approx root = [0.517638,1.931852]
Iteration 5: approx root = [0.517638,1.931852]
 

Trial 3

%pause
disp('Trial 3 of circle-hyperbola intersection problem')
x0 = [-3 1.5]';
disp(sprintf('Initial guess: x0 = [%f %f]',x0))
[root,iter] = newtonmv(x0, @circhyp_f, @circhyp_j, tol);
disp(' ')

Trial 3 of circle-hyperbola intersection problem
Initial guess: x0 = [-3.000000 1.500000]
Iteration 1: approx root = [-2.611111,-0.138889]
Iteration 2: approx root = [-2.053257,-0.412652]
Iteration 3: approx root = [-1.939689,-0.509855]
Iteration 4: approx root = [-1.931894,-0.517595]
Iteration 5: approx root = [-1.931852,-0.517638]
 

Trial 4

%pause
disp('Trial 4 of circle-hyperbola intersection problem')
x0 = [0 -3]';
disp(sprintf('Initial guess: x0 = [%f %f]',x0))
[root,iter] = newtonmv(x0, @circhyp_f, @circhyp_j, tol);

Trial 4 of circle-hyperbola intersection problem
Initial guess: x0 = [0.000000 -3.000000]
Iteration 1: approx root = [-0.333333,-2.166667]
Iteration 2: approx root = [-0.493939,-1.956061]
Iteration 3: approx root = [-0.517246,-1.932244]
Iteration 4: approx root = [-0.517638,-1.931852]
Iteration 5: approx root = [-0.517638,-1.931852]

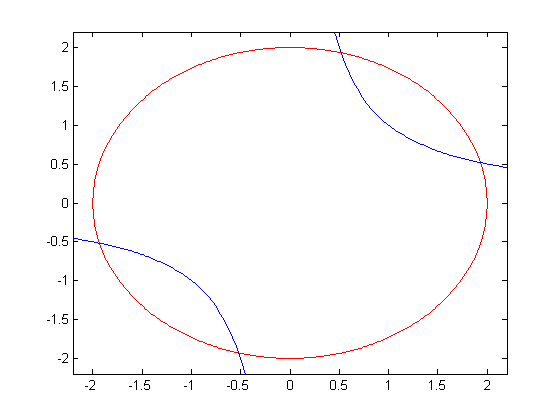
Plot solution

xi = -2:.02:2;
xi1 = -2.2:.02:-0.1;
xi2 = 0.1:.02:2.2;
plot(xi,sqrt(4-xi.^2),'r',xi,-sqrt(4-xi.^2),'r',...
    xi1,1./xi1,'b',xi2,1./xi2,'b')
axis([-2.2 2.2 -2.2 2.2])

© Greg Fasshauer, IIT. Published with MATLAB® 7.11