SplineDemo.m

Contents

Overview

Illustrates cubic spline interpolation by calling MATLAB's built-in spline function (for not-a-knot splines and clamped splines) and a modified version of splinetx (from NCM) (for natural splines). The functions evaluate the cubic spline interpolating the data specified in the vectors x and y at all of the points in the vector u.

As output we get plots of

Initialization

clear all
close all
% Define the data and evaluation points
x = [0 1 3 5 6];
y = [2 -3 1 2 4];
u = linspace(0,6,100);

Call splinetx_natural

Evaluate cubic natural spline interpolant at u

v = splinetx_natural(x,y,u);

Plots

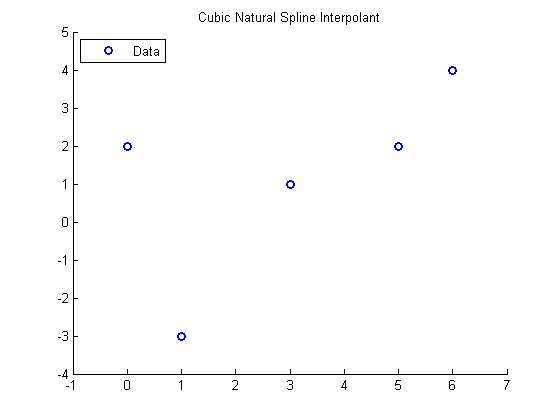
Plot the data

hold on
xlim([-1 7])
ylim([-4 5])
title('Cubic Natural Spline Interpolant')
plot(x,y,'bo','LineWidth',2)
legend('Data','Location','NorthWest')
pause

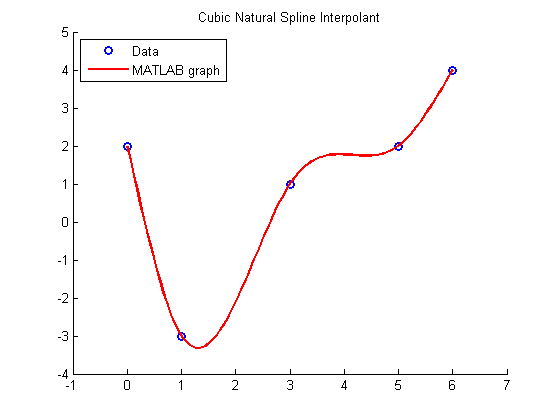
Use MATLAB to get a continuous graph

plot(u,v,'r','LineWidth',2)
legend('Data','MATLAB graph','Location','NorthWest')
hold off
pause

Call spline

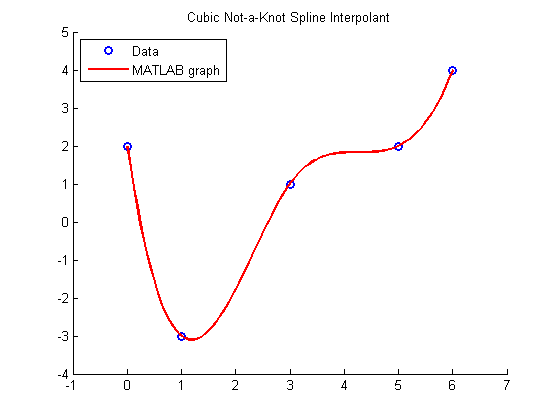
Evaluate cubic not-a-knot spline interpolant at u We could also use splinetx here.

v = spline(x,y,u);

Plots

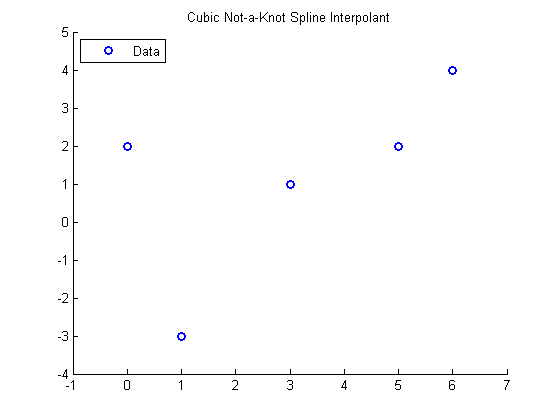
Plot the data

figure
hold on
xlim([-1 7])
ylim([-4 5])
title('Cubic Not-a-Knot Spline Interpolant')
plot(x,y,'bo','LineWidth',2)
legend('Data','Location','NorthWest')
pause

Use MATLAB to get a continuous graph

plot(u,v,'r','LineWidth',2)
legend('Data','MATLAB graph','Location','NorthWest')
hold off
pause

Call spline again

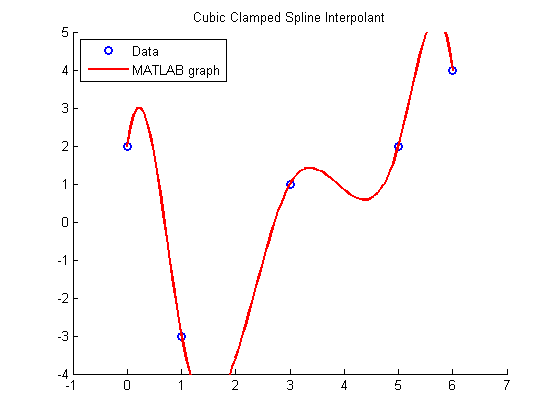
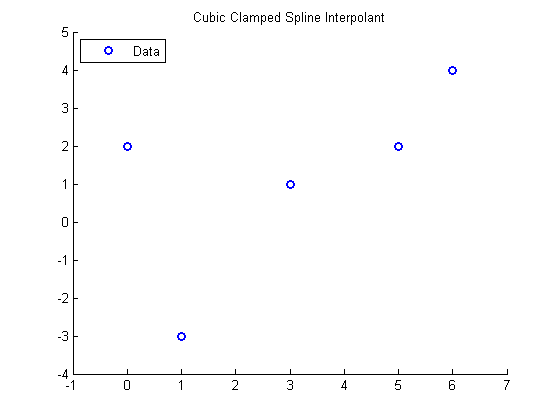
Repeat with cubic clamped spline defined in spline y(1) and y(end) contain the values of the slopes at left and right endpoints

y = [10 y -10];
% Evaluate cubic clamped spline interpolant at u
v = spline(x,y,u);

Plots

Plot the data

figure
hold on
xlim([-1 7])
ylim([-4 5])
title('Cubic Clamped Spline Interpolant')
plot(x,y(2:end-1),'bo','LineWidth',2)
legend('Data','Location','NorthWest')
pause

Use MATLAB to get a continuous graph

plot(u,v,'r','LineWidth',2)
legend('Data','MATLAB graph','Location','NorthWest')
hold off

Published with MATLAB® 7.9